Una distribuzione campionaria è una distribuzione relativa ad una specifica statistica calcolata su
più campioni di n dimensioni, tutti della stessa popolazione.
Per costruire una distribuzione campionaria occorre che ciascun campione
sia definito dallo stesso numero di casi n, ciascun campione di
ampiezza n sia estratto dalla stessa popolazione, l'estrazione sia
casuale e indipendente, e quindi si procede a calcolare la statistica e
la frequenza.
Distribuzione campionaria della proporzione di successi su n eventi dicotomici
Si contano i campioni per ciascun risultato, se ne calcola la statistica e si contano le frequenze.
Questo quando una distribuzione campionaria empirica.
Di solito però si fa riferimento ad una distribuzione campionaria teorica, costruita matematicamente con le regole della probabilità.
Come costruire una distribuzione campionaria teorica binomiale
- Definire il numero di elementi n che compongono ciascun campione
- Isolare l'evento singolo entro gli n che compongono il campione e stabilire la probabilità di successo p e quella di insuccesso q
- Definire tramite l'equazione binomiale le probabilità associate a tutti i risultati ottenibili con gli n elementi considerati (facendo variare k da 0 a n), calcolando la frequenza relativa attesa di ciascun risultato, cioè la proporzione di quanti campioni dovrebbero ottenere quel risultato
Distribuzione campionaria della media
Il teorema del limite centrale dice che indipendentemente dalla forma della distribuzione della popolazione, una distribuzione campionaria della media tende alla normalità all'aumentare di n e raggiunge la forma normale con n>=30.
Secondo la legge dei grandi numeri se n tende a N o all'infinito, la media di M tende a zero, perchè tutte le medie campionarie tendono a coincidere con la media della popolazione.
Quindi all'aumentare di n diminuisce la variabilità della distribuzione.
Proprietà della media campionaria:
- La sua forma è normale per n>=30
- la media è uguale a quella della popolazione
- la deviazione standard dipende da n
- Data la media della popolazione (µ), la media della distribuzione campionaria sarà uguale a quella della popolazione: µM = µ
- Data la deviazione standard della popolazione (σ), la deviazione standard della distribuzione campionaria, detta errore standard
(la media delle deviazioni di ciascun campione dalla media della
popolazione, cioè l'insieme degli scarti delle medie campionarie
rispetto al valore esatto della popolazione), si ottiene nei seguenti
modi:
- se la popolazione è infinita o il campione è prelevato con reinserimento:

- se la popolazione è finita e il campione è senza reinserimento:
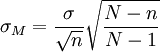
- se la popolazione è infinita o il campione è prelevato con reinserimento:
- Se la deviazione standard della popolazione non è nota, l'errore
standard può essere stimato utilizzando la statistica campionaria:
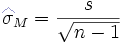
Dove il simbolino ^ indica che si tratta di una stima del parametro.
Per fare della statistica inferenziale si fa riferimento ai valori che stanno nelle aree estreme della distribuzione, nelle code della distribuzione.
Per la distribuzione normale si calcola il valore di z:
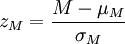
E andando poi a cercare il valore nella tavola della distribuzione normale standardizzata (Tavola 1b) si trova l'area limite.
In base ai risultati trovati si potrà infierire se si ha una buona stima del parametro della popolazione.
Attraverso le distribuzioni campionarie, si può cercare di stabilire il grado di esattezza del parametro stimato, trovando l'intervallo entro il quale ricade il parametro della popolazione, l'intervallo di fiducia.
Intervalli di fiducia della media
Se si conosce solo media e deviazione standard di un campione casuale, ma nessuna informazione sulla media della popolazione, si può fornire una stima intervallare, ovvero delimitare un intervallo di valori entro il quale dovrebbe ricadere il parametro.
Conoscendo la media del campione casuale, possiamo quindi ipotizzare che la media della popolazione sarà un valore poco maggiore o poco minore della media del campione, definendo un intervallo di fiducia, prendendo due limiti di fiducia, inferiore e superiore.
La fiducia viene quantificata a priori decidendo il livello, generalmente il 95% o il 99%, ovvero con probabilità uguale .95 o .99, ovvero delle probabilità molto alte.
Minore è la fiducia, e minore è la probabilità, ma maggiore è la precisione, maggiore è la fiducia, maggiore è la probabilità, ma minore è la precisione.
Tuttavia se abbiamo un campione non molto ampio e/o con una elevata deviazione standard, la nostra stima rischia di essere poco utile (ad esempio, se da un campione di voti da 18 a 30 fissiamo un intervallo di 20-29, risulterà una indicazione poco significativa).
Come calcolare l'intervallo di fiducia della media
- Calcolare l'errore standard della distribuzione campionaria della media
- Moltiplicare l'errore standard per z=1.96 se si sceglie il livello di fiducia del 95% o z=2.58 se si sceglie del 99%
- Per ottenere il limite inferiore, sottrarre il valore ottenuto dalla media campionaria:

- Ricavare i limite superiore sommando il valore ottenuto alla media campionaria:

- Riportare l'intervallo di fiducia del parametro della popolazione,
limite inferiore < µ < limite superiore
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon