Se in una ricerca sono stati presi in esame 2 campioni composti da
partecipanti con stesse caratteristiche generali, selezionati in maniera
casuale e indipendente, si parla di campioni indipendenti.
Questi campioni potranno essere diversi tra loro a seconda delle
esigenze dello sperimentatore che potrà deciderli di farli variare di
una specifica caratteristica ed ogni soggetto avrà un'unica misurazione.
Se invece si confronta un campione singolo per le sue coppie di valori
ottenute sullo stesso soggetto, ci si trova in un disegno entro soggetto
o anche detto di campioni dipendenti.
In questo caso ciascun soggetto avrà 2 misurazioni.
Lavorare con campioni dipendenti o indipendenti comporterà la scelta di usare test statistici differenti.
Nella distribuzione campionaria della differenza tra due medie, la media è uguale a zero:
µM1-M2=0
Mentre l'errore standard si calcola in relazione alla deviazione standard σ e alle ampiezze campionarie (n1 e n2):
Avendo due campioni da due differenti popolazioni, l'errore standard sarà calcolato in base alle deviazioni standard delle popolazioni e alle ampiezze campionarie:
In linea teoria, sia che i campioni provengano dalla stessa popolazione oppure da popolazioni diverse, una distribuzione campionaria della differenza tra due medie avrà le caratteristiche di una distribuzione normale nel caso in cui l'ampiezza campionaria di entrambi i campioni sia maggiore di 30.
Se invece almeno uno dei 2 campioni ha ampiezza minore di 30, avrà le caratteristiche di una distribuzione t student.
Ricapitolando:
µM1-M2 = µ-µ = 0
e
Verifica dell'ipotesi con due campioni indipendenti test z della differenza tra medie
- Prerequisiti:
a) I casi sono estratti in maniera indipendente e casuale e sono attribuiti casualmente ai 2 campioni
b) ciascun soggetto appartiene ad un solo campione, e quindi abbiamo 2 campioni indipendenti
c) la variabile dipendente che consideriamo è su scala metrica
d) i campioni hanno entrambi n>=30 - Si formulano le 2 ipotesi statistiche, quella nulla in termini di uguaglianza tra le medie (µ1=µ2 o µ1-µ2=0) e l'alternativa, che può essere bidirezionale o monodirezionale (sinistra o destra).
- Si fissa il livello di siglificatività α
- Si trovano sulla tavola 1b i valori critici di z in relazione al tipo di ipotesi fatta
- Si applica il test statistico z della differenza tra due medie:

Dove:
M1 e M2 sono le medie dei 2 campioni
s1 e s2 sono le deviazioni standard dei 2 campioni
n1 e n2 sono le ampiezze dei 2 campioni - Si prende una decisione in base a:
|Z| < |Zcritico| -> p>α -> Accetti H0
|Z| >= |Zcritico| -> p<=α -> Rifiuto H0
Dove |Z| vuol dire che è in valore assoluto (senza segno).
Verifica dell'ipotesi con due campioni indipendenti test t della differenza tra medie
- Prerequisiti:
a) I casi sono estratti in maniera indipendente e casuale e sono attribuiti casualmente ai 2 campioni
b) ciascun soggetto appartiene ad un solo campione, e quindi abbiamo 2 campioni indipendenti
c) la variabile dipendente che consideriamo è su scala metrica
d) almeno uno dei 2 campioni ha n<30 e/o la deviazione standard delle popolazioni non nota - Si formulano le 2 ipotesi statistiche, quella nulla in termini di uguaglianza tra le medie (µ1=µ2 o µ1-µ2=0) e l'alternativa, che può essere bidirezionale o monodirezionale (sinistra o destra).
- Si fissa il livello di siglificatività α
- Si trovano sulla tavola 2 i valori critici di t in relazione al tipo di ipotesi fatta, il livello di significatività di α, i gradi di libertà calcolati in base alle ampiezze campionarie n1 e n2:
gdl=n1+n2-2 - Si applica il test statistico t della differenza tra due medie:
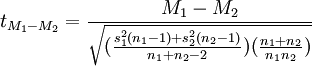
- Si prende una decisione in base a:
|t| < |t|critico| -> p>α -> Accetti H0
|t| >= |tcritico| -> p<=α -> Rifiuto H0
Intervalli di fiducia della differenza tra 2 medie
Intervallo di fiducia tra due medie con distribuzione normale
- Calcolare l'errore standard (deviazione standard)
- Moltiplicare l'errore standard per z=1.96 (livello di fiducia del 95%) o z=2.58 (livello di fiducia del 99%)
- Ottenere il limite inferiore con la seguente formula:

- Ottenere il limite superiore:
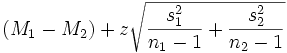
- Riportare l'intervallo di fiducia del parametro della popolazione per il livello di fiducia stabilito:
limite inferiore < µ1-µ2< limite superiore
- Calcolare l'errore standard (deviazione standard)
- Moltiplicare l'errore standard per t che:
a) con livello di fiducia del 95% va ricercato sulla tavola 2 con α=.05 e gdl=n1+n2-2
b) con livello di fiducia del 99% va ricercato sulla tavola 2 con α=.01 e gdl=n1+n2-2 - Ottenere il limite inferiore con la seguente formula:
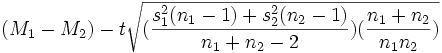
- Ottenere il limite superiore:

- Riportare l'intervallo di fiducia del parametro della popolazione per il livello di fiducia stabilito:
limite inferiore < µ1-µ2< limite superiore
Verifica dell'ipotesi con 2 campioni differenti: test t
Nel test entro soggetti si ricava prima la differenza tra ciascuna coppia di punteggi e poi se ne calcola la media, e la distribuzione di riferimento è la distribuzione campionaria della media delle differenze.
In questa distribuzione le medie sono calcolate su valori ottenuti per differenza da due misurazioni iniziali.
La media viene indicata con µD. -> µD=µ=0
L'errore standard σD:
Procedura verifica ipotesi test t della media delle differenze
-
Prerequisiti:
a) I casi che definiscono il campione devono essere estratti in maniera casuale ed indipendente dalla popolazione di riferimento.
b) Ciascun caso contribuisce con 2 misurazioni.
c) La variabile dipendente è su scala metrica -
Formare le ipotesi, quella nulla ponendo la differenza della media uguale a zero µD=0, quella alternativa bidirezionale o monodirezionale (diversa, maggiore o minore di zero)
-
Fissare il livello di signifcatività di α
-
Trovare nella tavola 2 i valori critici di t in base all'ipotesi alternativa, al livello di alfa e ai gradi di libertà, gdl=n-1
-
Applicare il test statistico della media delle differenze:

Dove gli indicatori MD e SD si calcolano così:
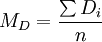
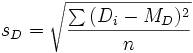
-
Si prende una decisione in base a:
|t| < |t|critico| -> p>α -> Accetti H0
|t| >= |tcritico| -> p<=α -> Rifiuto H0
Intervalli di fiducia della media delle differenze
I limiti di fiducia rappresentano i due valori entro i quali, con una probabilità del 95% o 99% (a seconda del α scelto) ci aspettiamo ricada il parametro della popolazione e si posson ricavare con la seguente formula:


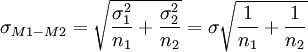

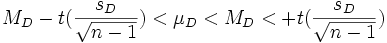
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon