L'analisi fattoriale ha lo scopo di individuare poche dimensioni non
osservabili che fan capire perchè certe variabili covariano.
L'analisi fattoriale vuole spiegare più covarianza possibile, cioè
rendere ragione al meglio delle correlazioni tra le variabili.
Analisi dei fattori principali (AFP)
In questo metodo vengono cercati dei fattori che spieghino più varianza
possibile delle variabili originali, con un procedimento identico a
quello del ACP, con la differenza che viene analizzata una matrice
ridotta Rh nella quale diagonale principale ci sono valori
inferiori a 1 che rappresentano stime di comunalità di ciascuna
variabile, quindi invece di analizzare tutta la varianza delle variabili
si analizza solo quella attribuibile ai fattori comuni.
L'AFP estrae il massimo di varianza per ogni fattore, i fattori vengono
individuati estraendo gli autovalori e gli autovettori di Rh.
L'AFP cerca quindi di spiegare la comunalità tra variabili facendo
ricorso a dimensioni latenti (non osservabili) che determinano le
relazioni tra le variabili osservate, inoltre l'AFP analizza solo la
varianza comune, la comunalità.
La matrice analizzata è composta da elementi fuori della diagonale che
riflettono la covarianza coppia a coppia (pairwise) tra le variabili, ed
elementi nella diagonale che riflettono la variabilità comune aggregata
(la comunalità).
Nell'AFP la soluzione fattoriale non è unica perchè può essere
influenzata molto dai valori iniziali di comunabilità scelti. e spesso
bastano pochi fattori a rendere ragione in maniera sostanziale delle
correlazioni tra le variabili.
Quindi, l'approccio delle componenti si concentra sull'approssimazione
della matrice dei punteggi osservati tramite un piccolo numero di
componenti, mentre quello dei fattori comuni enfatizza la riproduzione
della matrice delle correlazioni tra le variabili osservate.
Stime iniziali e valori di comunabilità
La prima cosa da fare nel metodo dell'AFP è quella di eliminare dalla
diagonale principale della matrice R la varianza unica di ciascuna
variabile, e dato che questa varianza è di solito non nota, bisogna
stimare la comunalità, tramite diversi approcci:
- Il coefficiente di correlazione più alto che una variabile ha con le altre variabili può essere un metodo su matrici di correlazioni molto grandi, ma non su quelle piccole.
- Il metodo b^2i=rikri1/rkl produce l'effetto di moderare le correlazioni troppo elevate.
- La correlazione media si basa sul calcolo della media delle correlazioni di una certa variabile i con tutte le altre variabili k contenute in R, e quindi:
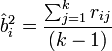
- Il coefficiente di correlazione multipla al quadrato (SMC), si ottiene considerando ogni variabile in R di volta in volta come variabile dipendente che regredisce sulle rimanenti variabili considerate come indipendenti, ed è il metodo maggiormente consigliato per la stima iniziale della comunalità.
Le comunalità vengono quindi sostituite alle stime iniziali e l'estrazione dei fattori si ripete, facendo nascere nuove saturazioni e comunalità, e si interrompe quando i valori empirici delle comunalità diventano sufficientemente stabili, cioè quando il valore delle comunalità ottenuto nel passaggio precedente non cambia in maniera sostanziale.
Durante questo processo, il numero di fattori deve rimanere costante.
Una volta che la soluzione fattoriale è stabilizzata, i valori finali delle comunalità possono essere ricavati elevando al quadrato le saturazioni di ogni variabile in ogni fattore comune, e sommando questi quadrati.
Alcuni problemi di questo processo è che possono eccedere i valori di comunalità (anche più del 100%), e questo può dipendere dal fatto che: i casi possono essere troppo pochi rispetto al numero di variabili analizzate, le stime delle comunalità possono essere molto distanti da quelle vere, il numero di fattori estratti può essere troppo elevato rispetto al numero necessario per rendere ragione di R.
Si hanno basse comunabilità quando ci sono variabili con basse correlazioni con altre variabili, e spesso la soluzione sta nell'eliminare queste variabili, o nell'introdurre altre variabili più correlate.
La stima iniziale delle comunalità può diventare via via meno importante all'aumentare della grandezza della matrice, perchè maggiore è il numero delle variabili analizzate e minore è il numero di elementi nella diagonale principale in rapporto a quello degli elementi fuori di essa.
Minimi quadrati
In questo metodo vengono minimizzate le correlazioni residue (R1-R^1), ovvero la parte di correlazione tra le variabili che non è spiegata dai fattori.
Viene inoltra massimizzata la riproduzione dei coefficienti fuori della diagonale principale di R1 e di solito si inizia stabilendo il numero di fattori da estrarre e si interrompe il processo quando lo scarto tra R1 e R^1 diviene molto piccolo.
Esistono 2 varianti del metodo:
- minimi quadrati ordinari (o non ponderati ULS):
FULS= SjSk(rjk-r^jk)2
Dove: R^jk=Spajpakp, p=1... m (numero fattori), ajp=saturazione della j-esima variabile nel p-esimo fattore - minimi quadrati generalizzati (GLS):
FGLS=SjSkSlSm ?jklm(rjk-r^jk)(rlm-r^lm)
Dove: ?jklm è un fattore di ponderazione ottenibile dal prodotto degli elementi bjk e blm nella inversa della matrice di correlazione.
All'inizio del processo di minimizzazione la funzione dei minimi quadrati viene trasformata così:

Dove F è la funzione FULS o FGLS
Questi metodi procedono ricalcolando comunalità e saturazioni fattoriali fino a che le funzioni dei mini quadrati non vengono minimizzate, cioè quando |R1-R^1|<e, con e molto piccolo, partendo di solito da una stima iniziale per le saturazioni fino a che la soluzione non migliora più.
Invece non è necessario fornire stime iniziali per le comunalità delle variabili, perchè questi metodi non usano le informazioni dentro la diagonale principale di R, e quindi la comunalità la ricavano alla fine del processo.
Massima verosomiglianza
Vengono individuate le saturazioni che rendono massima la probabilità di osservare dalla popolazione la matrice di R, individuando la soluzione fattoriale che meglio riproduce la matrice delle correlazioni R osservata, stimando le saturazioni della popolazione che hanno massima verosomiglianza nel produrre la matrice delle correlazioni campionaria R.
L'assunto di partenza è che i fattori latenti e le variabili osservate abbiano una distribuzione normale multivariata, e si usa questa funzione:
FML=tr(RC-1)+ln|C|-ln|R|-n
Dove: R è la matrice di correlazione, C è uguale a AA'+U2 ed è la matrice riprodotta dalla soluzione, n è il numero di variabili, | | indica il determinante e tr( ) la traccia della matrice.
In questo metodo si considerano solo gli elementi fuori della diagonale principale di R, quindi non serve una stima iniziale delle comunalità.
Test di bontà dell'adattamento (goodness of fit)
Viene usato per esaminare statisticamente l'adeguatezza della soluzione, dove i gradi di libertà di x2 vengono calcolati con df=[(n-k)2-(n+k)]/2, dove n è il numero di variabili e k il numero di fattori.
Se i gradi di libertà sono negativi vuol dire che non ci sono informazioni sufficienti per stimare i parametri e quindi non si può fare il test, in tal caso si dice che il modello d'analisi fattoriale non è identificativo.
Si esamina l'ipotesi nulla H0: R=R^, cioè se la matrice di correlazioni tra le variabili osservate R coincide con quella riprodotta dalla soluzione fattoriale R^=AA'+U2.
Se il valore di questa funzione non è significativo si accetta H0, e quindi non si estraggono più fattori.
Il valore di x2 viene ottenuto moltiplicando il valore finale della funzione di minimizzazione (FML o FGLS) per il numero di casi meno uno, tuttavia, se il campione è particolarmente piccolo, il test potrebbe risultare non significativo.
Indici alternativi di bontà dell'adattamento
Un problema vitale nell'uso del chi quadrato come test di bontà dell'adattamento è legato alla sua sensibilità alla numerosità del campione, per questo motivo sono stati sviluppati altri metodi/indici per verificare questa bontà d'adattamento, come:
Goodness of fit index: GFI=1-[tr(R^-1R-I)2/tr(R^-1R)2]
Adjusted Goodness of fit index: AGFI=1-[(q(q+1)/2df)(1-GFI)]
Dove q è il numero di variabili e df è il numero di gradi di libertà.
Questi indici variano da 0 a 1 e valutano la quantità di R che viene spiegata dalla matrice riprodotta R^, dove valori superiori a .9 indicano un buon adattamento.
Un altro indice alternativo è quello della radice quadrata della media dei residui al quadrato:
RMR=[2ΣiΣj(rij-r^ij)2/(q(q+1))]1/2
Dove rij e r^ij sono la correlazione osservata e la correlazione riprodotta tra le variabili i e j.
L'RMR indica la media della correlazione residua, non spiegata dal modello, ed indica un buon adattamento se il suo valore è piccolo (<.05).
L'indice di Tucker e Lewis si usa ipotizzando che non ci sia relazione tra variabili:
TLI=[(x2nullo/dfnullo)-(x2target/dftarget)]/ [(x2nullo/dfnullo)-1]
In questo modello, un coefficiente vicino ad 1 (>.9) indica un buon adattamento del modello ai dati empirici.
Un altro indice basato sul confronto con un modello nullo è quello dell'indice comparativo di adattamento, che si propone di stimare l'inadeguatezza del modello nella popolazione:
CFI=1-[max(x2target-dftarget'0)/max(x2nullo-dfnullo'x2target'0)]
Questo modello stima la bontà dell'adattamento nella popolazione e non su campione specifico, dove valori vicini ad 1 (>.9) indicano un buon adattamento ai dati.
L'indice RMSEA fornisce una stima dell'errore di approssimazione commesso quando la matrice delle correlazioni osservate R viene riprodotta dalla R^ ricavata dalle saturazioni di un determinato modello fattoriale.
RMSEA=[(x2-df)/N/df]1/2
Valori inferiori a .05 indicano un'errore minimo, da .05 e .08 l'errore è accettabile, mentre valori >.08 indicano che il modello fattoriale non regge.
Gli indici di accuratezza di Cliff sono indici applicabili ai risultati dell'analisi delle componenti principali e dell'analisi in fattori principali:

Dove: r è il numero di fattori estratti, q è il numero di variabili.
Un altro indice che rappresenta la media dei valori nella matrice di correlazione residua è:
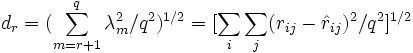
Se il valore di dr è circa uguale a 1/N (dove N=ampiezza campione) allora è probabile che la varianza residua consista principalmente in varianza dovuta all'errore campionario, e quindi che la soluzione fattoriale è adeguata.
Di questi modelli l'RMR sembra quello più sensibile a cattive specificazioni del modello: se un modello non è compatibile con i dati osservati perchè vengono specificati pochi fattori, l'indice RMR ha maggiori possibilità di rilevarlo rispetto agli altri indici.
Piaciuto l'articolo? Lascia un commento!
EmoticonEmoticon